Question

Assume you are planning a picnic for lunch, but when you woke up there were rain clouds in the sky. If 50% of rainy days start with rain clouds in the air, 20% of all days start with clouds in the air, and rain only typically occurs on 1 out of every 10 days, what is the probability that it will rain today and ruin your picnic

Answer 1

0.25 = 25% probability that it will rain today and ruin your picnic

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Cloudy skies

Event B: Rain

20% of all days start with clouds in the air

This means that
`P(A) = 0.2`

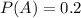
50% of rainy days start with rain clouds in the air

50% of 10%. So

`P(A \cap B) = 0.5*0.1 = 0.05`

What is the probability that it will rain today and ruin your picnic

`P(B|A) = (P(A \cap B))/(P(A)) = (0.05)/(0.2) = 0.25`

0.25 = 25% probability that it will rain today and ruin your picnic