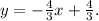Question

Write the equation of the line that passes through each pair of points (-2, 8) and (7, -4).

Answer 1

The equation of the line passing through (-2, 8) and (7, -4) is
`(y = -(4)/(3)x + (4)/(3)\)`, using the slope-intercept form y = mx + b.

To find the equation of the line passing through the points (-2, 8) and (7, -4), you can use the slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept.

First, calculate the slope m using the formula
`\(m = \frac{{y_2 - y_1}}{{x_2 - x_1}}\)`, where
`\((x_1, y_1)\)` and
`\((x_2, y_2)\)` are the coordinates of the two points.

`\[m = \frac{{-4 - 8}}{{7 - (-2)}} = \frac{{-12}}{{9}} = -(4)/(3)\]`

Now that you have the slope m, choose one of the points (let's use
(-2, 8)) to substitute into the equation. The y-intercept b can be found by rearranging the slope-intercept form:

`\[8 = (-(4)/(3)) * (-2) + b\]`

Solving for b:

`\[b = (4)/(3)\]`

The equation of the line is
`\(y = -(4)/(3)x + (4)/(3)\).`