Final Answer:
The measure of angle J (and angle L) is 90°, making the correct answer for angle x in Rectangle JKLM (c) 90°.
The correct answer is (c) 90°.
Step-by-step explanation:
In a rectangle, opposite angles are equal, and the sum of all interior angles is 360°. Since JKLM is a rectangle, angles J and L are opposite angles, and angles K and M are opposite angles. Therefore, angles J and L have the same measure, as do angles K and M.
Let's denote the measure of angle J
 Similarly, let's denote the measure of angle K (or angle M) as
Similarly, let's denote the measure of angle K (or angle M) as
 . Since opposite angles are equal,
. Since opposite angles are equal,

The sum of all interior angles in a rectangle is 360°. Therefore, we can write the equation:
![\[ \angle J + \angle K + \angle L + \angle M = 360° \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5t47sfe3houyx8e0uqenr5z0e64anjwt6l.png)
Substitute in the fact that
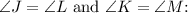
![\[ \angle J + \angle K + \angle J + \angle K = 360° \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jkdaalcb1shrkzx4l034iisnytkeiifj77.png)
Combine like terms:
![\[ 2\angle J + 2\angle K = 360° \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/og90sgbxdtsjx5xjcm8q4rvqadt5dczdja.png)
Divide both sides by 2:
![\[ \angle J + \angle K = 180° \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yiywwfeue0xg1dso2ikr9sxqoqbx7hxtrq.png)
Since
 we can rewrite this as:
we can rewrite this as:
![\[ \angle J + \angle L = 180° \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wogg07std5cxig22vavlo9x7ddnst8ko8k.png)
Now, since
 we can substitute:
we can substitute:
![\[ 2\angle J = 180° \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cq8h0d6ymz90gco4pahhd2td0kxhb7o1e4.png)
Divide both sides by 2:
![\[ \angle J = 90° \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gmzturkzjhegw4kz7jc5o5jpyyn1yj3231.png)
Therefore, the measure of angle J (and angle L) is 90°, making the correct answer for angle x in Rectangle JKLM (c) 90°.