Answer:
The new set of coordinates are
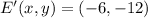 ,
,
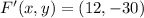 ,
,
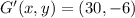 and
and
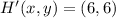 .
.
Explanation:
Vectorially speaking, dilation can be defined by this equation:
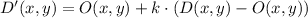 (1)
(1)
Where:
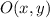 - Center of dilation.
- Center of dilation.
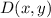 - Original point.
- Original point.
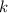 - Scale factor.
- Scale factor.
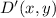 - Dilated point.
- Dilated point.
Let suppose that center of dilation is located at origin, we determine the new set of coordinates below:
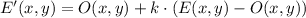
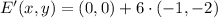
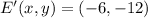
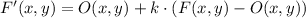
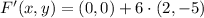
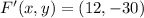
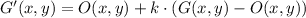
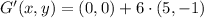
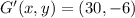
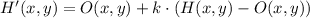
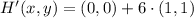
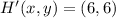
The new set of coordinates are
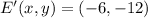 ,
,
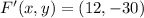 ,
,
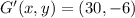 and
and
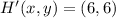 .
.