Question

A developer buys an empty lot to build a small house. What is the area of the lot? The graph shows a five-sided polygon. The five edges are on (0, 9), (7, 9), (9, 0), (0, minus 8), and (minus 10, 0). A. B. C. D.

Answer 1

The area of the polygon with vertices at (0, 9), (7, 9), (9, 0), (0, -8), and (-10, 0) is 45 square units.

To calculate the area of the five-sided polygon formed by vertices A(0, 9), B(7, 9), C(9, 0), D(0, -8), and E(-10, 0), you can divide it into two triangles and apply the Shoelace Formula.

1. **Triangle ABC:**

Use the Shoelace Formula with vertices A, B, and C:

`\[ \text{Area}_(ABC) = (1)/(2) \left| (0 * 9 + 7 * 0 + 9 * 9) - (9 * 7 + 0 * 0 + 0 * 9) \right| \]`

Simplifying,
`\(\text{Area}_(ABC) = (1)/(2) | 81 - 63 | = 9\).`

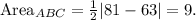
2. **Triangle ACD:**

Use the Shoelace Formula with vertices A, C, and D:

`\[ \text{Area}_(ACD) = (1)/(2) \left| (0 * 0 + 9 * (-8) + 0 * 9) - (9 * 0 + (-8) * 0 + 0 * 0) \right| \]`

Simplifying,
`\(\text{Area}_(ACD) = (1)/(2) | -72 - 0 | = 36\).`

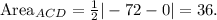
Now, sum the areas of both triangles:

`\[ \text{Total Area} = \text{Area}_(ABC) + \text{Area}_(ACD) = 9 + 36 = 45 \]`

Therefore, the area of the lot is 45 square units.