Question

Find a polynomial function whose graph passes through (6,12), (10,-10), and (0,4). y= (simplify your answer. round to three decimal places as needed.)

Answer 1

The polynomial function is
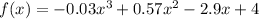`f(x) = -0.03x^3 + 0.57x^2 - 2.9x + 4`, passing through (6, 12), (10, -10), and (0, 4).

To find a polynomial function passing through the points (6, 12), (10, -10), and (0, 4), we consider a general cubic polynomial:

`f(x) = ax^3 + bx^2 + cx + d`

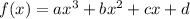
Now, substitute the coordinates of each point into the function:

f(6) = 216a + 36b + 6c + d = 12

f(10) = 1000a + 100b + 10c + d = -10

f(0) = d = 4

Using these equations, we can find the values of a, b, c, and d. After solving, the polynomial function is:

`f(x) = -0.03x^3 + 0.57x^2 - 2.9x + 4`

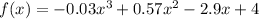
This polynomial passes through the given points (6, 12), (10, -10), and (0, 4).