Question

Pls find 16 and 17 !
16 - AB
17 - m work needs to be shown

Answer 1

In the given right-angled triangle with base AT = 12 and height BT = 6, applying the Pythagorean theorem yields the hypotenuse

`\(AB = 6√(5)\)` units. In another scenario involving tangent circles and angles, the measure of angle ∠TDC is found to be 74° when x = 9°.

In a right-angled triangle, the Pythagorean theorem can be used to find the length of the hypotenuse (the side opposite the right angle). The Pythagorean theorem is given by:

`c^2 = a^2 + b^2`

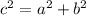
where:

- c is the length of the hypotenuse,

- a and b are the lengths of the other two sides.

In your case, the base of the triangle is AT = 12 and the height is BT = 6. Let's denote the hypotenuse as AB = c .

`\[ c^2 = 12^2 + 6^2 \]`

`\[ c^2 = 144 + 36 \]`

`\[ c^2 = 180 \]`

Now, take the square root of both sides to find \( c \):

`\[ c = √(180) \]`

`\[ c = √(36 * 5) \]`

`\[ c = 6 √(5) \]`

So, the length of the hypotenuse \( AB \) is
`\( 6 √(5) \)` units.

17. Since AB and CD are tangent to circle O at points B and C, we know that ∠ABO and ∠CDO are right angles.

We can also see that ∠ABT and ∠CDT are inscribed angles that subtend the same arc, BD. Therefore, we know that ∠ABT = ∠CDT.

We can use the same logic to find that ∠TBC = ∠ADC.

Now, let's consider triangle ACD. We know that
∠ACD + ∠ADC + ∠CAD = 180° (because the sum of the angles in a triangle is 180°). We can also substitute ∠TBC and ∠ABT for ∠ACD and ∠ADC, respectively. So, we have:

∠TBC + ∠ABT + ∠CAD = 180°

Substitute in the values we know:

(4x + 4)° + (8x + 2)° + 66° = 180°

Combine like terms:

12x + 72° = 180°

Subtract 72° from both sides:

12x = 108°

Divide both sides by 12:

x = 9°

Substitute 9° for x in the expression for ∠TDC:

m∠TDC = (8 * 9°) + 2°

Calculate:

m∠TDC = 72° + 2°

Therefore, m∠TDC = 74°.