Question

A spherical buoy of radius R = 4 feet floats in a calm lake. Half of a foot of the buoy is submerged. Place a coordinate system with the origin at the center of the sphere. (a) Find an equation of the sphere. (Use (x, y, z) for coordinates. Assume the positive z-axis corresponds to the up direction.) (b) Find an equation of the circle formed at the waterline of the buoy.

Answer 1

(a) The equation of the sphere is
`\(x^2 + y^2 + (z - 4)^2 = 16.\)` (b) The equation of the circle formed at the waterline of the buoy is
`\(x^2 + y^2 = 16.\)`

Step-by-step explanation:

(a) The equation of a sphere with radius R and center at (h, k, l) is given by
`\((x - h)^2 + (y - k)^2 + (z - l)^2 = R^2.\)` In this case, the buoy is a spherical object with radius R = 4 feet, and since half a foot is submerged, the center is at (0, 0, 4 - 0.5) = (0, 0, 3.5). Substituting these values into the general equation, we get
`\(x^2 + y^2 + (z - 3.5)^2 = 16.\)`

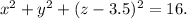
(b) The circle formed at the waterline is the intersection of the sphere with the plane z = 3.5. Substituting z = 3.5 into the equation of the sphere, we get
`\(x^2 + y^2 = 16,\)` which represents the equation of the circle formed at the waterline of the buoy. This circle lies in the xy-plane and has a radius of 4 feet, consistent with the original sphere's radius.

These equations describe the geometric relationship between the buoy and the waterline circle in the given coordinate system, providing a mathematical representation of their positions in three-dimensional space.