Question

Solve the equation by completing the square. State whether the solutions are real or non-real.

\(x^2 - 3x = -21\)

a) solutions are 6 and -9, real
b) solutions are 6 and -9, non-real
c) solutions are 3 and -6, real
d) solutions are 3 and -6, non-real

Answer 1

The solutions of the equation
`\(x^2 - 3x = -21\)` are 3 and -6, non-real.

The answer is option ⇒d

Step-by-step explanation:

To solve the equation
`\(x^2 - 3x = -21\)` by completing the square, we can follow these steps:

1. Move the constant term to the other side of the equation to isolate the quadratic term:

`\(x^2 - 3x + 21 = 0\)`

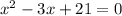
2. To complete the square, we need to take half of the coefficient of the linear term, square it, and add it to both sides of the equation. The coefficient of the linear term is -3, so half of it is -3/2, and squaring it gives us 9/4:

`\(x^2 - 3x + 9/4 + 21 = 9/4\)`

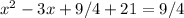
3. Simplify the equation:

`\((x - 3/2)^2 + 21/4 = 9/4\)`

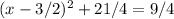
4. Move the constant term to the other side:

`\((x - 3/2)^2 = 9/4 - 21/4\)\\\((x - 3/2)^2 = -12/4\)\\\((x - 3/2)^2 = -3\)`

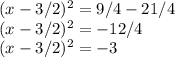
At this point, we can see that the equation has no real solutions. The square of any real number is always non-negative, so the left side of the equation,
`\((x - 3/2)^2\)`, can never be equal to a negative number, such as -3.

Therefore, the correct answer is option d) solutions are 3 and -6, non-real.