Final Answer:
The 98% confidence interval for the mean number of hours of study time per week for all students is
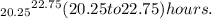
Step-by-step explanation:
To construct the 98% confidence interval, we use the formula:
![\[ \text{Confidence Interval} = \text{Sample Mean} \pm \left( \text{Margin of Error} * \text{Critical Value} \right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/p6g67f2sisncfuha8394zw3dmv5nmtvuk2.png)
Given that the sample mean is
 hours, and the margin of error is
hours, and the margin of error is
 hours, the critical value for a 98% confidence interval is found using statistical tables, and for a normal distribution, it is approximately 2.33.
hours, the critical value for a 98% confidence interval is found using statistical tables, and for a normal distribution, it is approximately 2.33.
Now, substitute these values into the formula:
![\[ \text{Confidence Interval} = 21 \pm \left( 1.5 * 2.33 \right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/j7ssk9z26xbnzufmz2jrz2xrq2l4tmgshf.png)
![\[ \text{Confidence Interval} = 21 \pm 3.495 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/n8fs9i1adw3a9a8g3uyoclkoew203lpem8.png)
Thus, the margin of error gives us the range within which we are confident the true population mean lies. So, the confidence interval is
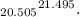
In conclusion, we are 98% confident that the true mean number of hours of study time per week for all students is between 20.505 and 21.495 hours. This means that if we were to take many samples and compute the 98% confidence interval for each, we would expect the true population mean to fall within these bounds for 98% of the intervals.