Question

The mode ofa continuous random variable having density f is the value of x for which f(x) attains its maximum. Compute the mode of X in cases (a), (b), and (c) of Theoretical Exercise 5.13?

Answer 1

The mode of the continuous random variable (X) with density function (f) in cases (a), (b), and (c) of Theoretical Exercise 5.13 is as follows:

(a) Mode of (X) in case (a):
`\(x_{\text{mode, (a)}} = a\)`

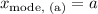
(b) Mode of (X) in case (b):
`\(x_{\text{mode, (b)}} = (a + b)/(2)\)`

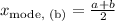
(c) Mode of (X) in case (c):
`\(x_{\text{mode, (c)}} = b\)`

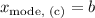
Step-by-step explanation:

In case (a), the mode
`(\(x_{\text{mode, (a)}}\))` is equal to the lower bound (a) since f(x) attains its maximum at (a). This is because in a continuous distribution, the mode is the value where the probability density function reaches its peak.

In case (b), the mode (
`\(x_{\text{mode, (b)}}\))` is the midpoint of the interval (a, b), calculated as
`\((a + b)/(2)\).`This occurs when the density function is symmetrically distributed, and the maximum value is at the center of the interval.

In case (c), the mode
`(\(x_{\text{mode, (c)}}\))`is equal to the upper bound (b) since (f(x) attains its maximum at (b). Similar to case (a), this is because the probability density function reaches its peak at the upper bound.

To understand this intuitively, consider the shape of the density function for each case. In case (a), it is left-skewed, peaking at (a); in case (b), it is symmetrically distributed, peaking at the midpoint; and in case (c), it is right-skewed, peaking at (b). These characteristics determine the mode in each scenario, aligning with the points of maximum density in the respective distributions.