Question

Find the indicated probabilities using the geometric​distribution, the Poisson​ distribution, or the binomial distribution. Then determine if the events are unusual. If​convenient, use the appropriate probability table or technology to find the probabilities. The mean number of oil tankers at a port city is 11 per day. The port has facilities to handle up to 15 oil tankers in a day. Find the probability that on a given​ day,

(a) eleven oil tankers will​ arrive,
(b) at most three oil tankers will​ arrive, and​
(c) too many oil tankers will arrive. ​
(a) ​P(eleveneleven oil tankers will ​arrive)= ​(Round to four decimal places as​ needed.)
​(b) P(at most three oil tankers will ​arrive)= ​(Round to four decimal places as​ needed.) ​
(c) P(too many oil tankers will ​arrive)= ​(Round to four decimal places as​ needed.)
A.The event in part​ (a) is unusual.
B.The event in part​ (b) is unusual.
C.The event in part​ (c) is unusual.
D.None of the events are unusual.

Answer 1

To solve this problem, we'll use the Poisson distribution formula:

`\[ P(X=k) = (e^(-\lambda) \cdot \lambda^k)/(k!) \]`

where
`\lambda` is the mean number of events per time period.

Given:
`Mean (\( \lambda \)) = 11`

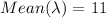
(a) Probability that exactly eleven oil tankers will arrive P(X=11):

`\[ P(X=11) = (e^(-11) \cdot 11^(11))/(11!) \]`

(b) Probability that at most three oil tankers will arrive
`(\( P(X \leq 3) \))`:

`\[ P(X \leq 3) = \sum_(k=0)^(3) (e^(-11) \cdot 11^k)/(k!) \]`

(c) Probability that too many oil tankers will arrive
`(\( P(X > 15) \))`:

`\[ P(X > 15) = 1 - P(X \leq 15) \]`

Now, calculate these probabilities using a calculator or software. After obtaining the values, we can assess if the events are unusual based on a threshold significance level.