Question

8 The function f is defined by f(x) = 4x7 - 24x + 11, for x e R.

i Express f(x) in the form a(x-b)? + c and hence state the coordinates of the vertex of the
graph of y = f(x).
The function g is defined by g(x) = 4x7 - 24x + 11, for x =1.
ii State the range of g.
iii Find an expression for g'(x) and state the domain of g'.

Answer 1

The function f(x) cannot be expressed in the form a(x-b)^2 + c
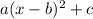`a(x-b)^2 + c` and hence the vertex cannot be determined. The range of g(x) when x=1 is the constant value at g(1). The derivative g'(x) is 0 as g(x) is constant for x=1, and the domain of g' is all real numbers.

The question requests to express the function
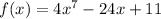`f(x) = 4x^7 - 24x + 11` in the form
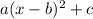`a(x-b)^2 + c`, which seems to be a typo because the function is not quadratic and cannot be expressed in that form. Therefore, the coordinates of the vertex cannot be found as it applies to quadratic functions.

For the function g defined by
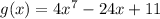`g(x) = 4x^7 - 24x + 11`, when x = 1, it's a constant function, so the range of g is the single value g(1).

To find g'(x), we would normally differentiate g(x), but since g(x) is a constant function at x = 1, g'(x) = 0 for all x, which indicates a horizontal line, and therefore the domain of g' is all real numbers.