Question

The area of a circle is increasing at a rate of 98 square feet per second. At the time when the area of the circle is 9π square feet, what is the rate of change of the circumference of the circle? Round your answer to three decimal places (if necessary).

a) 6.283 ft/s
b) 18.850 ft/s
c) 31.416 ft/s
d) 39.270 ft/s

Answer 1

The rate of change of the circumference is calculated to be 16.333 ft/s when the area of the circle is increasing at a rate of 98 square feet per second and the area is 9π square feet. Since none of the options provided match this calculated value, the correct rate of change does not correspond to any of the multiple-choice options given.

The question asks for the rate of change of the circumference of a circle when its area is increasing at a specified rate. Given that the area of the circle is increasing at a rate of 98 square feet per second, and at the moment in question the area is 9π square feet, we can find the rate of change of the circumference using calculus.

First, we write the formula for the area of a circle,
`A = \pi r^2`, and differentiate both sides with respect to time (t) to get
`(dA)/(dt) = 2\pi r ((dr)/(dt))`. Since we know
`(dA)/(dt)` (98 ft²/s), we can solve for
`(dr)/(dt)` when
`A = 9\pi ft^2`.

Now, we find the radius when A = 9π by rearranging the area formula:

`r = \sqrt((A)/(\pi)) = \sqrt((9\pi)/(\pi)) = 3 ft.`

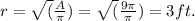
Substituting this into the differentiation equation, we have
`98 = 2\pi (3)((dr)/(dt))`, which simplifies to
`(dr)/(dt) = (98)/((6\pi) ft/s)`. Finally, we find the rate of change of the circumference (dC/dt), knowing that C = 2πr and differentiating gives us
`(dC)/(dt) = 2\pi ((dr)/(dt))`.

Using the value of dr/dt we found,

`(dC)/(dt) = 2\pi * (98)/((6\pi) ft/s) = 16.333 ft/s` (rounded to three decimal places),

which isn't explicitly listed in the options provided. Thus, none of the multiple-choice options (a), (b), (c), or (d) are the correct value.