Question

What equation will show the manager's transportation spending limits? Replace the inequality sign with the equal sign. Use the Graph tool to graph the resulting equation and paste it into the box below. Describe which part of the graph should be shaded and whether the line should be dashed or not.

Answer 1

The manager's transportation spending limits can be represented by the solid line equation
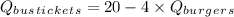`Q_b_u_s _t_i_c_k_e_t_s = 20 - 4 * Q_b_u_r_g_e_r_s`, with a vertical intercept of 20 and a slope of -4. There is no shading involved since the inequality has been replaced by an equality.

The equation that shows the manager's transportation spending limits is derived by taking the inequality that represents the manager's budget constraint and replacing the inequality sign with an equal sign. For Alphonso's scenario:

`Budget = \$10 = \$2 * quantity of burgers + \$0.50 * quantity of bus tickets`

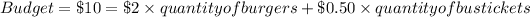
By isolating the quantity of bus tickets, we get:

`\$10 - \$2 * Qburgers = \$0.50 * Qbus tickets`

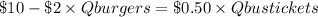
Turning this into the equation of a line, we have:

`Q_b_u_s _t_i_c_k_e_t_s = (\$10)/(\$0.50) - (\$2)/(\$0.50) * Q_b_u_r_g_e_r_s`

`Q_b_u_s _t_i_c_k_e_t_s = 20 - 4 * Q_b_u_r_g_e_r_s`

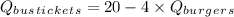
This gives us a line with a vertical intercept of 20 and a slope of -4. If the line represents a strict limit, it will be a solid line; if it's possible to spend less than the limit, the line would be dashed. Since the inequality has been replaced with an equal sign, the line should be solid. The shaded area would normally be below the line to indicate all possible combinations of burgers and bus tickets within the budget, but since we're only graphing the equation as a line, no shading is applicable here.