Question

Find the area of the shaded sector of the circle​

Answer 1

The area of the shaded sector of the circle is found by calculating the proportion of the full circle's area corresponding to an angle of 110 degrees. Given the full circle's area as
`60m^2`, the shaded sector's area is about
`18.33m^2`.

To find the area of the shaded sector of a circle when the area of one half of the circle is given to be
`30m^2`, and the angle formed by a line intersecting the diameter is 110 degrees, we use the concept that the area of a sector is proportional to its angle.
Firstly, we know that the area of the full circle is twice the area of the half-circle given, which is

`2 * 30m^2 = 60m^2`.

The area A of a circle is given by,

`A = \pi r^2`,

thus,

`60m^2 = \pi r^2`,

and we can solve for
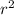`r^2` as
`r^2 = 60m^2 / \pi`.

The entire circle has an angle of 360 degrees, and the shaded sector corresponds to an angle of 110 degrees.

Therefore, the area of the shaded sector is
`((110)/(360)) * \pi r^2`, which after substituting for r2 gives us
`((110)/(360)) * 60 m^2`. Simplifying this, we find that the area of the shaded sector is approximately 18.33m2.