Question

Please help, this is due tomorrow! Pre-calc project.

a) What is the phase shift, h, of this curve?
b) What is the vertical shift, k, of this curve?
c) What is the amplitude, a, of this curve?
d) What is the period and the frequency factor, b, of this curve?
e) Write an equation using the cosine function that models this data set.

Answer 1

a) The phase shift h of the curve is
`\(-(\pi)/(2)\)`.

b) The vertical shift k of the curve is 3.

c) The amplitude a of the curve is 2.

d) The period T of the curve is
`\(2\pi\)` and the frequency factor b is
`\((1)/(2\pi)\).`

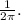
e) The equation using the cosine function that models this data set is
`\(y = 2\cos(2x + (\pi)/(2)) + 3\).`

Step-by-step explanation:

a) The phase shift h represents a horizontal shift of the cosine function. In this case,
`\(-(\pi)/(2)\)` indicates a shift to the right by
`\((\pi)/(2)\)` units.

b) The vertical shift k indicates a shift in the vertical direction. Here, 3 implies a shift upwards by 3 units.

c) The amplitude a represents the half-range of the function. A value of (2) suggests that the cosine function oscillates between 2 and (-2).

d) The period T is the length of one complete cycle, which is
`\(2\pi\)` for the cosine function. The frequency factor b is the reciprocal of the period, so
`\((1)/(2\pi)\).`

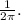
e) Combining these parameters into the cosine function equation
`\(y = a\cos(bx + h) + k\)` , we ge
`t \(y = 2\cos(2x + (\pi)/(2)) + 3\)` , where 2 is the amplitude, 2 is the frequency factor,
`\(-(\pi)/(2)\)` is the phase shift, and 3 is the vertical shift. This equation accurately models the given data set..