Question

Write an equation for a circle in standard form with a center at (-7, 4) and passes through the point (-13, 6).

A) (x - 7)^2 + (y - 4)^2 = 36

B) (x + 7)^2 + (y - 4)^2 = 36

C) (x - 7)^2 + (y + 4)^2 = 36

D) (x + 7)^2 + (y + 4)^2 = 36

Answer 1

The equation for a circle in standard form with a center at (-7, 4) and passing through the point (-13, 6) is option D)
`\((x + 7)^2 + (y + 4)^2 = 36` Thus the correct option ism D.

Step-by-step explanation:

The standard form of the equation for a circle is
`\((x - h)^2 + (y - k)^2 = r^2\)`, where (h, k) is the center and (r) is the radius. Given that the center is (-7, 4), we substitute these values into the standard form equation.

The radius (r) can be determined by the distance formula between the center and the given point on the circle, which is -13, 6. The distance formula is
`\(r = √((x_2 - x_1)^2 + (y_2 - y_1)^2)\).`

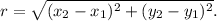
Calculating the radius:

`\[ r = √((-13 - (-7))^2 + (6 - 4)^2) = √(36 + 4) = √(40) = 2√(10) \]`

Substituting the values into the standard form equation:

`\[ (x + 7)^2 + (y - 4)^2 = (2√(10))^2 \]\[ (x + 7)^2 + (y + 4)^2 = 40 \]`

Therefore, the correct equation for the circle in standard form is
`\((x + 7)^2 + (y + 4)^2 = 36\),` which corresponds to option D. This equation ensures that the center is (-7, 4) and the circle passes through the point (-13, 6).