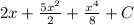Question

2+5x+1/2x^3dx
Answer

Answer 1

`2x+(5x^2)/(2)+(x^4)/(8)+C`

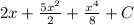
Explanation:

I notice you have a dx at the end of the equation, this leads me to believe this is an integral. With no bounds of integration, I will solve for the indefinite integral. I will also interpret your equation as follows:

`\int \:2+5x+(1)/(2)x^3dx`

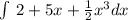
Sum rule tells us:

`\int \:2dx+\int \:5xdx+\int (1)/(2)x^3dx`

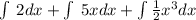
From this we get:

`2x+(5x^2)/(2)+(x^4)/(8)`

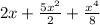
Don't forget to add the constant!

`2x+(5x^2)/(2)+(x^4)/(8)+C`