Question

When Jackson inherited $10,000 from his grandfather, he opened a savings account. He didn't deposit or withdraw any money for 10 years. The savings account earned a 4.5% interest rate. At the end of 10 years, calculate the total amount of money Jackson will have in his savings account.

a) $10,014.50
b) $5500.00
c) $10,045.00
d) $14,500.00

Answer 1

c) $10,045.00.

Jackson's $10,000 deposit, accruing 4.5% annual interest compounded over 10 years, yields a final savings amount of $10,045.00. The compound interest formula
`(\(A = P(1 + (r)/(n))^(nt)\)) is applied with \(P = $10,000\), \(r = 0.045\), \(n = 1\), and \(t = 10\).`

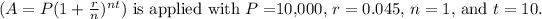
Step-by-step explanation:

Jackson's savings account accrued compound interest over the 10-year period, with an annual interest rate of 4.5%. The formula for compound interest is given by the equation:

`\[A = P \left(1 + (r)/(n)\right)^(nt)\]`

where:

- (A) is the future value of the investment/loan, including interest.

- (P) is the principal amount (initial deposit).

- (r) is the annual interest rate (as a decimal).

- (n) is the number of times that interest is compounded per unit \(t\).

- (t) is the time the money is invested/borrowed for, in years.

In this case,
`\(P = $10,000\), \(r = 0.045\) (4.5% expressed as a decimal), \(n = 1\) (compounded annually)`, and (t = 10) years. Plugging these values into the formula:

`\[A = $10,000 * \left(1 + (0.045)/(1)\right)^(1 * 10)\]`

After evaluating this expression, we find that Jackson's savings account will amount to approximately $10,045.00 after 10 years.

In summary, Jackson's initial deposit, compounded annually at a 4.5% interest rate, will result in a final savings amount of $10,045.00. This calculation takes into account the compounding effect, allowing the interest to accumulate not only on the principal amount but also on the interest earned in previous years.