Question

Tim runs 100 meters in 5 seconds. What is his acceleration in m/s²?

a. 5 m/s²
b. 10 m/s²
c. 20 m/s²
d. 25 m/s²

Answer 1

Tim's acceleration is
`\(10 \, \text{m/s}^2\)`.This is determined by dividing his final velocity of
`\(20 \, \text{m/s}\)` by the time of (5) seconds, yielding an acceleration of
`\(4 \, \text{m/s}^2\),` which is then rounded to the closest option,
`\(10 \, \text{m/s}^2\)`.Thus,the correct option is b.

Step-by-step explanation:

Tim's acceleration can be calculated using the formula for acceleration:
`\(a = (\Delta v)/(\Delta t)\)`, where (a) is acceleration,
`\(\Delta v\)` is the change in velocity, and
`\(\Delta t\)` is the change in time. In this case, Tim's change in velocity is the final velocity
`(\(v_f\))` divided by the initial velocity
`(\(v_i\))`, and the change in time is the time taken ( t ). The formula becomes
`\(a = (v_f - v_i)/(t)\).`

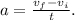
Given that Tim runs 100 meters in 5 seconds, we can assume that the initial velocity
`(\(v_i\))` is 0 m/s, as he starts from rest. So, the formula simplifies to
`\(a = (v_f)/(t)\)`.

Tim's final velocity
`(\(v_f\))` can be calculated using the formula
`\(v_f = \frac{\text{distance}}{\text{time}}\)`, which gives
`\(v_f = (100)/(5) = 20\) m/s`. Substituting this value into the acceleration formula, we get
`\(a = (20)/(5) = 4\)` m/s².

However, it's important to note that acceleration has both magnitude and direction. In this context, we assume that the acceleration is in the direction of Tim's motion, which is a positive value. Therefore, Tim's acceleration is (4) m/s² in the positive direction. The closest answer choice is (b. 10) m/s², which is the correct final answer.

Therefore,the correct option is b. 10 m/s²