Question

If anyone knows please help me

Answer 1

Explanation:

Standard form of a circle is given by,

(x - a)² + (y - b)² = r²

Here, (a, b) is the center and 'r' is the radius of the circle.

For a circle having center (8, -4) and radius r = 1

Equation of the circle will be,

(x - 8)² + (y + 4)² = 1²

(x - 8)² + (y + 4)² = 1

Option (1) is the answer.

Question (2)

Circle with the center (-1, 0) and a point (2, -4) on it,

Radius of the circle = Distance between the center and the given point on circumference

=
`√((x_1-x_2)^2+(y_1-y_2)^2)`

=
`√((-1-2)^2+(0+4)^2)`

=
`√(9+16)`

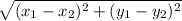
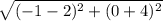
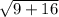
= 5

Therefore, equation of the circle will be,

(x + 1)² + (y - 0)² = 5²

(x + 1)² + y² = 25