Question

Find the total surface area of this cylinder.

Give your answer to 1 decimal place.
7 cm
15 cm

Answer 1

For the first figure :

Cylinder :

Radius =7cm

height = 15cm

Total Surface Area:

2 \times \pi \times r(h + r)2×π×r(h+r)

= 2×22/7×7 (15+7)

= 22×44

= 968 cm sq.or 9.68m sq.

For the second figure :

Diameter = 24cm (radius= 24/2= 12cm)

•Height = 18 cm

Total Surface area:

2 \times \pi \times r(h + r)2×π×r(h+r)

= 2×22/7×12 (18+12)

= 2×22/7×12 (30)

= 2×22×12×5

= 2640 cm. sq or 26.4 m.sq

Answer 2

The total surface area of the cylinder is approximately
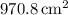`\(970.8 \, \text{cm}^2\)` when rounded to one decimal place. The calculation is based on a cylinder with a radius of 7 cm and a height of 15 cm. The formula used is
`\(2\pi r^2 + 2\pi rh\).`

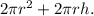
Explanation:

To find the total surface area of a cylinder, you can use the formula:

`\[ \text{Surface Area} = 2\pi r^2 + 2\pi rh \]`

where:

( r ) is the radius of the base of the cylinder,

( h ) is the height of the cylinder.

In your case, you've provided the dimensions:

Radius ( r ) = 7 cm

Height ( h) = 15 cm

Now, plug these values into the formula:

`\[ \text{Surface Area} = 2\pi(7)^2 + 2\pi(7)(15) \]`

`\[ \text{Surface Area} = 2\pi(49) + 2\pi(105) \]`

`\[ \text{Surface Area} = 98\pi + 210\pi \]`

`\[ \text{Surface Area} = 308\pi \]`

Now, you can calculate the numerical value:

`\[ \text{Surface Area} \approx 970.8 \, \text{cm}^2 \]`

So, the total surface area of the cylinder is approximately
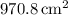`\( 970.8 \, \text{cm}^2 \)` (to 1 decimal place).