Question

For positive integer n, the factorial notation n! represents the product of the integers from n to 1. (For example, 6! = 6*5*4*3*2*1.) What value of n satisfies the following equation?

5! X 9! = 12! x N

Answer 1

The value of N that satisfies the equation is
`(1)/(11)`

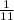
Explanation:

First we open the factorial of 12, to simplify the expression:

12! = 12*11*10*9!

So

5!*9! = 12!*N

5!*9! = 12*11*10*9!N

12*11*10N = 5!

Now we open the factorial of 5. So

12*11*10*N = 5*4*3*2*1

Since 5*2 = 10, 4*3 = 12, we have that:

12*11*10*N = 10*12*1

Now, simplifying by 10*12

11N = 1

`N = (1)/(11)`

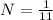
This is the value of N that satisfies the equation