Question

Please help 25p- it’s urgent

Answer 1

p = 20, q = 20, r = 30

Explanation:

The triangle to the left of OA is isosceles ( 2 equal radii ), then the base angles are congruent, so

p = 20

The 3 angles in this triangle sum to 180°, then the angle at O is

180 - (20 + 20) = 180 - 40 = 140°

AB is a straight line so angle in triangle containing q is 180 - 140 = 40

The triangle containing q is also isosceles ( 2 equal radii ) then base angles are congruent, then

q =
`(180-140)/(2)` =
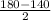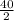`(40)/(2)` = 20

The triangle to the right of OA is also isosceles ( 2 equal radii ) then the base angles are congruent, so

r = 30

Then p = 20, q = 20, r = 30