Final Answer:
a) Question 1 (a) -
 , Question 1 (b) -
, Question 1 (b) -
 , Question 2 - Efficiency = 80.00%
, Question 2 - Efficiency = 80.00%
Step-by-step explanation:
Question 1:
(a) To find the number of secondary turns
 , we use the turns ratio formula:
, we use the turns ratio formula:
![\[ (N_p)/(N_s) = (V_p)/(V_s) \]](https://img.qammunity.org/2024/formulas/physics/high-school/zo7s8br4fco6raozmf75v6z99kbwhomng9.png)
Given
 turns and
turns and
 , and
, and
 for the motor, we can solve for
for the motor, we can solve for
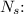
![\[ (1500)/(N_s) = (120)/(24) \]](https://img.qammunity.org/2024/formulas/physics/high-school/1ldizqdmma1w1pygf1m3jwucbozokr3gcn.png)
![\[ N_s = 1200 \]](https://img.qammunity.org/2024/formulas/physics/high-school/lyawt53f53x4l8dmyzmt65xas0couu2cfn.png)
(b) To find the primary current
 , we use the formula:
, we use the formula:
![\[ I_p = (V_p)/(Z) \]](https://img.qammunity.org/2024/formulas/physics/high-school/ey77fqljd4t0eqd8fdh6px217oe3ttiznh.png)
Where (Z) is the total impedance. For an ideal transformer, (Z) is only resistive and is given by:
![\[ Z = (V_p)/(I_p) \]](https://img.qammunity.org/2024/formulas/physics/high-school/mhv3bdbygvb9brmsppxa0j6z9tkxljc9l1.png)
Given
 and
and
 we can calculate (Z) and then find
we can calculate (Z) and then find
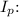
![\[ Z = (120V)/(7.5A) = 16 \Omega \]](https://img.qammunity.org/2024/formulas/physics/high-school/2j4cql2elxdcn11zonttegyu5bij7gv8yc.png)
![\[ I_p = (120V)/(16 \Omega) = 7.5A \]](https://img.qammunity.org/2024/formulas/physics/high-school/u7zrf6w9zbm5cgc4gul9bgtmzhcyih59az.png)
Question 2:
The efficiency
 of a transformer is given by the formula.
of a transformer is given by the formula.
The output power is the product of voltage and current on the secondary side, and the input power is the sum of copper losses and iron losses:
![\[ \eta = \frac{V_s \cdot I_s}{V_p \cdot I_p + \text{Copper Losses} + \text{Iron Losses}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/vjq13obo6c4txt61av86gcv8i1phbwehgc.png)
Given the values, we can calculate the efficiency:
![\[ \eta = (250V \cdot 100A)/(250V \cdot 100A + 450W + 225W) \]](https://img.qammunity.org/2024/formulas/physics/high-school/r2wlkibvn37nt8jjyhq02n7ljuquelmo1m.png)
![\[ \eta \approx 80.00\% \]](https://img.qammunity.org/2024/formulas/physics/high-school/6ne2zpgtueo05q6qtr973glcghiu9m9r1h.png)