Question

Find the exact values of the six trigonometric ratios in reduced form for angle A if a=6 and c= 12.

a) sin(A) = 1/2, cos(A) = √3/2, tan(A) = √3/3, csc(A) = 2, sec(A) = 2√3/3, cot(A) = √3
b) sin(A) = √3/2, cos(A) = 1/2, tan(A) = √3, csc(A) = 2√3/3, sec(A) = 2, cot(A) = 1/√3
c) sin(A) = 1/2, cos(A) = √3/2, tan(A) = √3, csc(A) = 2, sec(A) = 2√3/3, cot(A) = 1/√3
d) sin(A) = √3/2, cos(A) = 1/2, tan(A) = √3/3, csc(A) = 2√3/3, sec(A) = 2, cot(A) = √3

Answer 1

This is determined by finding the missing side using the Pythagorean theorem and calculating the trigonometric ratios using the given sides. Thus the correct option is c) sin(A) = 1/2, cos(A) = √3/2, tan(A) = √3, csc(A) = 2, sec(A) = 2√3/3, cot(A) = 1/√3.

Step-by-step explanation:

Given that
`\(a = 6\)`and
`\(c = 12\)`, we can find \(b\) using the Pythagorean theorem:
`\(a^2 + b^2 = c^2\).` Substituting the values, we get
`\(6^2 + b^2 = 12^2\),`which simplifies to
`\(36 + b^2 = 144\).` Solving for
`\(b\),` we get
`\(b = √(108) = 6√(3)\).`

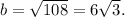
Now, we can calculate the trigonometric ratios:

`- \( \sin(A) = (a)/(c) = (6)/(12) = (1)/(2) \)`

`- \( \cos(A) = (b)/(c) = (6√(3))/(12) = (√(3))/(2) \)- \( \tan(A) = (a)/(b) = (6)/(6√(3)) = (√(3))/(3) \)- \( \csc(A) = (1)/(\sin(A)) = (1)/(1/2) = 2 \)- \( \sec(A) = (1)/(\cos(A)) = (1)/(√(3)/2) = (2√(3))/(3) \)- \( \cot(A) = (1)/(\tan(A)) = (1)/(√(3)/3) = (1)/(√(3)/3) * (√(3))/(√(3)) = (1)/(√(3)/3) * (√(3))/(√(3)) = (√(3))/(3) \)`

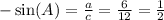
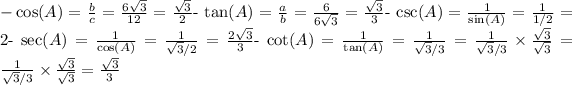
Hence, the correct answer is option c) with the provided trigonometric ratios in reduced form. Thus the correct option is c) sin(A) = 1/2, cos(A) = √3/2, tan(A) = √3, csc(A) = 2, sec(A) = 2√3/3, cot(A) = 1/√3.