Given:
The two points on the graph are R(-2,-4) and S(-8,-6).
To find:
The length of RS.
Solution:
Distance formula: The distance between two points is
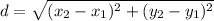
Using the distance formula, the distance between R(-2,-4) and S(-8,-6) is
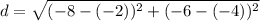
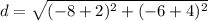
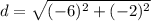
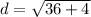
On further simplification, we get
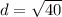
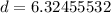
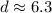
Therefore, the length of AB is about 6.3 units. So, the correct option is C.