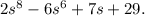Question

What is the polynomial in standard form for the expression 29 + 7s - 6s^6 + 2s^8?

a. 2s^8 - 6s^6 + 7s + 29
b. 2s^8 + 7s - 6s^6 + 29
c. 29 - 6s^6 + 7s + 2s^8
d. 2s^8 - 6s^6 + 29 + 7s

Answer 1

The polynomial in standard form for the expression
`29 + 7s - 6s^6 + 2s^8` is
`2s^8 - 6s^6 + 7s + 29`.

The answer is option ⇒A

Step-by-step explanation:

To write the polynomial expression
`29 + 7s - 6s^6 + 2s^8` in standard form, we arrange the terms in descending order based on their exponents.

The standard form of a polynomial is given by combining like terms and arranging them in descending order.

In this case, the polynomial in standard form for the given expression is:

`2s^8 - 6s^6 + 7s + 29.`

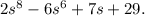
The terms are arranged in descending order based on their exponents, with the highest degree term
`(2s^8)` first and the constant term
`(29)` last.

Therefore, the correct polynomial in standard form for the expression
`29 + 7s - 6s^6 + 2s^8` is:

`2s^8 - 6s^6 + 7s + 29.`

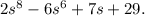
Therefore, the correct answer is option a)
`2s^8 - 6s^6 + 7s + 29.`