Question

Please help answer question​

Answer 1

C = 1.01

Step-by-step explanation:

Given that,

Mass, m = 75 kg

The terminal velocity of the mass,
`v_t=60\ m/s`

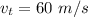
Area of cross section,
`A=0.33\ m^2`

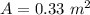
We need to find the drag coefficient. At terminal velocity, the weight is balanced by the drag on the object. So,

R = W

or

`(1)/(2)\rho CAv_t^2=mg`

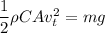
Where

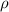`\rho` is the density of air = 1.225 kg/m³

C is drag coefficient

So,

`C=(2mg)/(\rho Av_t^2)\\\\C=(2* 75* 9.8)/(1.225* 0.33* (60)^2)\\\\C=1.01`

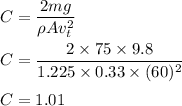
So, the drag coefficient is 1.01.