Question

It would be 5 m right? because thats when she started slowing down ?

Answer 1

125 m

Step-by-step explanation:

When given a time vs. velocity graph, the distance travelled will be the area under the curve.

Why? Recall that
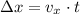`\Delta x=v_x\cdot t` which relates to the classic
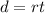`d=rt` equation (total displacement is equal to the average velocity multiplied by the time).

In this case, from 0 seconds to 5 seconds, we have a convenient rectangle. Finding the area of the rectangle is simple, recall that the area of a rectangle is length x width.

The width of the velocity is 25 m/s. This means that the student was driving at a constant speed of 25 m/s the entire time, which means her average velocity for the period of 5 seconds must have been 25 m/s. Perfect.

We want the total distance she travelled from 0 seconds to 5 seconds, which is a total of 5 seconds of driving.

Now multiply:

`\text{Area}_(rectangle)=25\cdot 5=\boxed{125\text{ m}}`

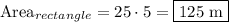
Therefore, she travelled 125 m during the first five seconds of motion.

*Extra note regarding why 5 m isn't correct:

Remember we are looking at a time vs velocity graph. She starts slowing down at t=5s (5 seconds after she started driving), but that doesn't mean she travelled 5 meters. Imagine you start driving, from rest, at an average velocity of 30 m/s for 10 seconds. Just because you start to slow down 10 seconds after driving doesn't mean you travelled 10 meters. Seconds are not meters! Remember, in a time vs velocity graph, if you want to find total distance travelled from a certain interval, find the area under the curve between that interval.