Question

To solve the equation \(8\left(\frac{1}{4}x-3\right)+24=4\left(x+5\right)\), we can follow these steps:

Step 1: Distribute the 8 and 4 to simplify the equation:
\(2x - 24 + 24 = 4x + 20\)

Step 2: Combine like terms:
\(2x = 4x + 20\)

Step 3: Subtract 4x from both sides:
\(2x - 4x = 20\)

Step 4: Simplify:
\(-2x = 20\)

Step 5: Divide both sides by -2:
\(x = -10\)

Therefore, the solution to the equation is \(x = -10\).

Answer 1

The solution to the equation
`\(8\left((1)/(4)x-3\right)+24=4\left(x+5\right)\) is \(x = -10\).`

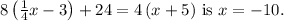
Step-by-step explanation:

To solve the given equation, we follow a series of steps. In Step 1, we distribute the constants 8 and 4 to the terms inside the parentheses, simplifying the equation. In Step 2, we combine like terms on both sides of the equation, resulting in
`\(2x = 4x + 20\).` Moving to Step 3, we subtract 4x from both sides, yielding
`\(-2x = 20\)`. Finally, in Step 5, we divide both sides by -2 to isolate x, finding
`\(x = -10\).`

This solution makes sense when we analyze the steps. Distributing and combining like terms are standard algebraic manipulations to simplify expressions. Subtracting 4x from both sides isolates the x term on one side, and dividing by -2 solves for x. Checking our solution, we substitute
`\(x = -10\)`back into the original equation to ensure it holds true. This step is crucial in validating the solution and confirming that our algebraic steps are accurate.

Therefore, through systematic algebraic manipulations, we arrive at the solution
`\(x = -10\)`, ensuring the equation is balanced on both sides and holds true for the given values.