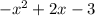Final answer:
The sum of the given polynomials
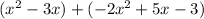 in standard form is
in standard form is
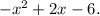
The answer is option ⇒E
Step-by-step explanation:
To sum polynomials, align like terms and add them together, and the sum should be in standard form as ax² + bx + c. To find the sum of the given polynomials in standard form, we simply combine like terms.
Let's simplify the expression step by step:
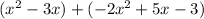
Combine the like terms of
 :
:
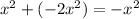
Combine the like terms of
 :
:
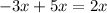
Combine the constant terms:
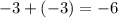
Putting it all together, the simplified sum of the polynomials is:
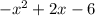
Therefore, the correct answer is E)
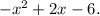
Your question is incomplete, but most probably the full question was:
What is the sum of the given polynomials in standard form?
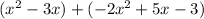
A)

B)
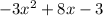
C)

D)
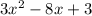
E)