Question

Graph the functions. Find all rational zeros. Include multiplicities and points in between zeros.

7. f(x) = x5 + 4x4 + x3 – 10x2 - 4x + 8

Answer 1

The graph of the function
`\( f(x) = x^5 + 4x^4 + x^3 - 10x^2 - 4x + 8 \)`exhibits multiple changes in direction, potentially indicating the presence of multiple zeros.

Step-by-step explanation:

To find the rational zeros, we consider the Rational Root Theorem, which states that any rational root of a polynomial must be a factor of the constant term divided by a factor of the leading coefficient. For this polynomial, the constant term is 8, and the leading coefficient is 1. The factors of 8 are ±1, ±2, ±4, ±8, and the factors of 1 are ±1. Therefore, the potential rational zeros are
`\( \pm 1, \pm 2, \pm 4, \pm 8 \).`

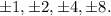
To determine which of these are actual zeros, we can use synthetic division or polynomial long division. By trying each potential zero, we find the actual zeros and their multiplicities. The graph will have x-intercepts at these zeros, and the multiplicity indicates how many times the factor contributes to the zero.

The final step is to plot the graph of the function using the identified zeros and their multiplicities. Additionally, points between zeros can be calculated to observe the behavior of the function in those regions. This comprehensive approach provides a detailed understanding of the function's characteristics, including the location and nature of its zeros.