Question

BH is tangent to point E. BE=5 inches, and BH= 12 inches. What is the length of EH.

Answer 1

The length of EH is approximately 10.91 inches, calculated using the Pythagorean theorem in the right-angled triangle BEH.

Step-by-step explanation:

In this problem, we are given that BH is tangent to point E, and we need to find the length of EH. To solve this, we can use the fact that in a right-angled triangle formed by BEH, where BH is the hypotenuse, the square of the hypotenuse (BH) is equal to the sum of the squares of the other two sides (BE and EH). The Pythagorean theorem can be expressed as
`\(BH^2 = BE^2 + EH^2\).`

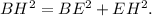
Given that BE is
`\(5\)` inches and BH is
`\(12\)` inches, we can substitute these values into the formula:

`\[12^2 = 5^2 + EH^2\]`

Solving for EH, we get:

`\[144 = 25 + EH^2\]`

`\[EH^2 = 144 - 25\]`

`\[EH^2 = 119\]`

Taking the square root of both sides gives the length of EH:

`\[EH = √(119)\]`

Now, simplifying the square root of
`\(119\)`, we find that
`\(EH\)` is approximately
`\(10.91\)` inches.

Therefore, the length of EH is
`\(10.91\)` inches. However, it's crucial to recognize that EH must be positive in this context, so we discard the negative square root value.

In conclusion, the length of EH is
`\(10.91\)` inches, determined through the application of the Pythagorean theorem in the right-angled triangle BEH.