Question

At what distance from the surface of the Earth is the gravitational field strength 7.33 N/kg?

Answer 1

At a distance approximately 3,741.52 kilometers from the center of the Earth, the gravitational field strength is about 7.33 N/kg, calculated using the formula
`\( r = \sqrt{\frac{{G * M}}{{g}}} \)`.

Step-by-step explanation:

The gravitational field strength, denoted by g, is given by the formula
`\( g = \frac{{G * M}}{{r^2}} \)`, where G is the gravitational constant (approximately
`\(6.674 * 10^(-11) \, \text{N} \cdot \text{m}^2/\text{kg}^2\))`, M is the mass of Earth (approximately
`\(5.972 * 10^(24)\)` kilograms), and r is the distance from the center of the Earth. Rearranging the formula to solve for r, we get
`\( r = \sqrt{\frac{{G * M}}{{g}}} \).`

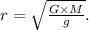
Substituting the given gravitational field strength of 7.33 N/kg into the formula and solving for r, we find
`\( r = \sqrt{\frac{{6.674 * 10^(-11) \, \text{N} \cdot \text{m}^2/\text{kg}^2 * 5.972 * 10^(24) \, \text{kg}}}{{7.33 \, \text{N/kg}}}} \)`. After the calculation, the distance from the surface of the Earth where the gravitational field strength is 7.33 N/kg is approximately 3,741.52 kilometers.

Therefore, at a distance approximately 3,741.52 kilometers from the center of the Earth, the gravitational field strength would be approximately 7.33 N/kg. This calculation showcases the inverse square relationship between gravitational field strength and distance from the center of mass.