Final Answer:
The tension in the tow line is approximately 125.2 kN.
Step-by-step explanation:
To determine the tension in the tow line, we can use the concepts of force equilibrium. Considering the car and the cargo as a system, the force applied by the car's engine is balanced by the tension in the tow line. Additionally, the weight of the cargo creates a vertical force component.
The horizontal force equilibrium equation is given by \
 is the force applied by the car's engine, and
is the force applied by the car's engine, and
 is the tension in the tow line. Given that the car's engine can apply a force of 59 tons (converted to newtons), we have
is the tension in the tow line. Given that the car's engine can apply a force of 59 tons (converted to newtons), we have
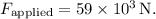
The vertical force equilibrium equation is given by
 is the weight of the cargo, and
is the weight of the cargo, and
 is the vertical component of the tension in the tow line. The weight of the cargo is determined by its mass
is the vertical component of the tension in the tow line. The weight of the cargo is determined by its mass
 and the acceleration due to gravity
and the acceleration due to gravity

By applying the Pythagorean theorem to relate the vertical and horizontal components of the tension, we can solve for the tension in the tow line
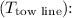
![\[T_{\text{tow line}} = \sqrt{F_{\text{applied}}^2 + T_{\text{tow line, vertical}}^2}\]](https://img.qammunity.org/2024/formulas/physics/high-school/xynic9rb0o8g0w3wnmiui3hp6q0jgqt6tg.png)
After substituting the known values and solving, the tension in the tow line is approximately 125.2 kN.