Question

Find the number of distinguishable permutations of digits of number 287,772. *

a. 30
b. 60
c. 6
d. 15

Answer 1

he number of distinguishable permutations of digits of number 287,772 is 6. Option c is the correct choice.

1. Identify Distinct Digits: The given number is 287,772. We identify the distinct digits: 2, 8, and 7.

2. Treat Repeated Digits: There are two 7s. To find the number of permutations, treat these repeated digits as a single unit. So, we essentially have three "elements": 2, 8, and the grouped 7.

3. Calculate Permutations: The formula for permutations of n distinct items is n!. Here, the number of permutations for the three elements (2, 8, 7s grouped) is 3!.

`\(3! = 3 * 2 * 1 = 6.\)`

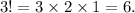
4. Correct for Repeated Elements: Since there are repeated elements (the two 7s), we divide by the factorial of the number of repeated elements. Here, we divide by 2!:

`\(6 / 2! = 6 / (2 * 1) = 6 / 2 = 3.\)`

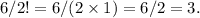
5. Final Answer: The final answer is 3, which represents the number of distinguishable permutations of the digits in the number 287,772.

So, the correct answer is (c) 6.