The function p(x) increases on (-5, 1), decreases on
 , is concave up on (-5, -2), and concave down on
, is concave up on (-5, -2), and concave down on
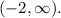
The function p(x) exhibits specific behaviors on different intervals:
1. Increasing Interval: (-5, 1) - On this interval, the function p(x) is increasing, indicating that as x increases, the values of p(x) also increase.
2. Decreasing Interval:
 - On this interval, the function p(x) is decreasing, signifying that as x increases, the values of p(x) decrease.
- On this interval, the function p(x) is decreasing, signifying that as x increases, the values of p(x) decrease.
3. Concave Up Interval: (-5, -2) - The function p(x) is concave up on this interval, suggesting that the graph is shaped like a cup, and its rate of increase is increasing.
4. Concave Down Interval:
 - On this interval, p(x) is concave down, indicating a graph shaped like an upside-down cup, with a decreasing rate of increase.
- On this interval, p(x) is concave down, indicating a graph shaped like an upside-down cup, with a decreasing rate of increase.
These descriptions provide insights into the directional trends and curvature of the function p(x) across different intervals.