The solution to the initial value problem
 with
with
 is
is
 , where C = 31.
, where C = 31.
Let's simplify the given differential equation using the provided substitution
 :
:
1. Find the derivatives u' and y':
![\[u' = 2x + 2yy'\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vrx5lz9yxe28ulxv201cjjixdzkesukpq2.png)
![\[y' = (u' - 2x)/(2y)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5rvdpkwgltqpbru8n7sd0gnvb99s94naqk.png)
2. Substitute into the given differential equation:
![\[y\left((u' - 2x)/(2y)\right) + x = √(x^2 + y^2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/el6nlcekpw1vnmm2ml1r6h7v7o436qptpw.png)
3. Simplify by canceling common terms:
![\[(1)/(2)u' - x = √(x^2 + y^2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ftywq0vywq3xu52g18jm8tx62ogjg6p3mn.png)
4. Square both sides to eliminate the square root:
![\[(1)/(4)u'^2 - xu' + x^2 = x^2 + y^2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ygvi5tggbgrybum6kid0jypg0mwflmyunm.png)
5. Substitute back
 :
:
![\[(1)/(4)u'^2 - xu' + u = u\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ped9xtm2c5a74esls0bf7asmlw3trip01p.png)
6. Simplify further:
![\[(1)/(4)u'^2 - xu' = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b1iqpmdz74hrrqpz3cla0lrsdynhh7bx61.png)
7. Solve for u':
u' - 4x = 0
u' = 4x
8. Integrate u' with respect to x to find u:
![\[u = 2x^2 + C\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/g1ojrgc7eo024f6v9jlo1cv6ank7prwwue.png)
9. Substitute back
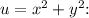
![\[x^2 + y^2 = 2x^2 + C\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/t60sh8w6ujkx4it3hvpiihiz3dyh22aocj.png)
10. Solve for y:
![\[y^2 = x^2 + C\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/h98ccd7icbaufme4760j6i06v2x9cp1rus.png)
![\[y = \pm √(x^2 + C)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/j32lrw0zmk9msj5symoj2fy7bjbs3jkzz3.png)
This is the solution to the given initial value problem, where C is the constant of integration.