Final answer:
The likelihood ratio test statistic for testing
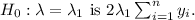
Step-by-step explanation:
In statistical hypothesis testing, the likelihood ratio test evaluates the likelihood of the null hypothesis
 against an alternative hypothesis by comparing their likelihood functions. For the exponential distribution, the likelihood function is \
against an alternative hypothesis by comparing their likelihood functions. For the exponential distribution, the likelihood function is \
 are observed values. To test
are observed values. To test
 we construct the likelihood ratio test statistic.
we construct the likelihood ratio test statistic.
The likelihood under the null hypothesis, denoted as
 The likelihood under the alternative hypothesis is \(L(\hat{\lambda}) =
The likelihood under the alternative hypothesis is \(L(\hat{\lambda}) =
 is the maximum likelihood estimate of
is the maximum likelihood estimate of

The likelihood ratio test statistic is the ratio of the likelihoods under the null and alternative hypotheses, i.e.,
 . Simplifying this ratio gives
. Simplifying this ratio gives
 Taking the logarithm of this ratio yields
Taking the logarithm of this ratio yields
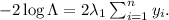
This
 statistic follows a chi-squared distribution with 1 degree of freedom. It is used to decide whether to reject or fail to reject the null hypothesis based on the significance level and critical values.
statistic follows a chi-squared distribution with 1 degree of freedom. It is used to decide whether to reject or fail to reject the null hypothesis based on the significance level and critical values.