Question

Hello there !

Can I have some help with this question? Thank you !

Answer 1

About 6 hours.

Explanation:

The cylinder has a diameter of 10 meters and a depth of 1.4 meters.

First, we can find the volume of the cylinder, given by the formula:

`V=\pi r^2h`

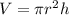
Where r is the radius and h is the height (or depth, in this case).

Since our diameter is 10, our radius is 5.

Therefore, the volume of the cylinder will be (using 3.14 as π):

`V=(3.14)(5)^2(1.4)=109.9\text{ meters} ^3`

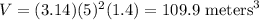
Since water is pumped at a rate of 18 cubic meters per hour, it will take then:

`109.9/18=6.10\overline{5}\approx 6\text{ hours}`

So, it will take about 6 hours for the water to completely fill the pool.