Question

at a processing plant, olive oil of density 875 kg/m3 flows in a horizontal section of hose that constricts from a diameter of 3.20 cm to a diameter of 1.25 cm. assume steady, ideal flow.(a) what is the volume flow rate if the change in pressure between the two sections of hose is 4.90 kpa?

Answer 1

The volume flow rate of olive oil is 0.00310 m³/s.

Given:

Density of olive oil, ρ=875 kg/m³

Diameter of hose at inlet,
`d_1` =3.20 cm = 0.032 m

Diameter of hose at outlet,
`d_2` =1.25 cm = 0.0125 m

Change in pressure between inlet and outlet, ΔP=−4900 Pa (note that the pressure change is negative since the flow is from a higher pressure to a lower pressure)

Assumptions:

Steady, ideal flow

Incompressible fluid

Calculate the area of the hose at the inlet and outlet:

`A_1` = π(
`d_(1/2)`)² = π(0.032/2)² = 8.0425 × 10⁻⁴ m²

`A_2` = π(
`d_(2/2)`)² = π(0.0125/2)² = 1.5708 × 10⁻⁴ m²

Apply Bernoulli's equation to relate the pressure, velocity, and density at the inlet and outlet:

`P_1 + (1/2)\rho v_1^2= P_2 + (1/2)\rho v_2^2`

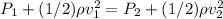
Since the flow is horizontal, the change in elevation is negligible, and we can set the potential energy terms to zero.

Rearrange Bernoulli's equation to solve for the velocity at the inlet:

`v_1 = √( [(2(P_1 - P_2)) / \rho])`

Substitute the given values:

`v_1 = √([(2(-4900)) / (875)])` = 3.90 m/s

Calculate the volume flow rate at the inlet:

Q =
`v_1A_1` = (3.90)(8.0425 × 10⁻⁴) = 0.00310 m³/s