Question

Describe the steps you would take to graph this equation:
Y-4=4/3 = {(x + 2)

Answer 1

Main Answer:

To graph the equation
`\(y - 4 = (4)/(3)(x + 2)\),` the first step is to rewrite it in slope-intercept form
`(\(y = mx + b\)).`

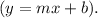
Step-by-step explanation:

To graph the equation
`\(y - 4 = (4)/(3)(x + 2)\)`, we need to transform it into the slope-intercept form
`(\(y = mx + b\))`, where
`\(m\)` is the slope and
`\(b\)` is the y-intercept. Begin by distributing
`\((4)/(3)\)`to both terms inside the parentheses, resulting in
`\(y - 4 = (4)/(3)x + (8)/(3)\)`. Next, isolate
`\(y\)`by adding 4 to both sides of the equation, giving
`\(y = (4)/(3)x + (8)/(3) + 4\)`. Combine the constants on the right side to simplify, yielding the final equation
`\(y = (4)/(3)x + (20)/(3)\)`, which is in slope-intercept form.

Now, the slope
`(\((4)/(3)\))` indicates the rise over run, and the y-intercept
`(\((20)/(3)\))`is the point where the line intersects the y-axis. By plotting the y-intercept and using the slope to identify additional points, you can graph the equation accurately on a coordinate plane. Understanding and applying these steps ensures a clear visualization of the linear relationship represented by the given equation.