In the air-standard Brayton cycle with a pressure ratio of 15, initial conditions are:
 . Net work output is approximately 459.07 kJ/kg, heat input is about 446.57 kJ/kg, and entropy generation is around 0.372 kJ/(kg·K).
. Net work output is approximately 459.07 kJ/kg, heat input is about 446.57 kJ/kg, and entropy generation is around 0.372 kJ/(kg·K).
(a) Determine the pressure and temperature at the beginning of each process:
1. Isentropic Compression (Process 1-2):
- Given:
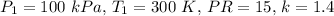
- Using
 , we find
, we find
 and
and
 :
:
![\[ P_2 = 1500 \ kPa, \ T_2 = 557.89 \ K \]](https://img.qammunity.org/2024/formulas/engineering/college/mzkde5urhvo5viq35c40ie9iw4z425ktxm.png)
2. Isobaric Heat Addition (Process 2-3):
-
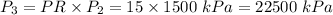
-
 (given)
(given)
3. Isentropic Expansion (Process 3-4):
- Using
 , we find
, we find
 and
and
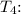
![\[ P_4 = 1500 \ kPa, \ T_4 = 442.62 \ K \]](https://img.qammunity.org/2024/formulas/engineering/college/w9cvbh736ho2yrkt2kktmk02as94qec4pv.png)
4. Isobaric Heat Rejection (Process 4-1):
-
 (given)
(given)
-
 (given)
(given)
(b) Calculate Net Work Output and Heat Input:
![\[ W_(net) = C_p \cdot (T_3 - T_2) - C_p \cdot (T_4 - T_1) \]\[ Q_(in) = C_p \cdot (T_3 - T_2) \]](https://img.qammunity.org/2024/formulas/engineering/college/uawiyvpycr2rwu3c5x1xex00r7qv4s5ekm.png)
Using
 :
:
![\[ W_(net) = 1.004 \cdot (1000 - 557.89) - 1.004 \cdot (442.62 - 300) \]\[ W_(net) \approx 459.07 \ kJ/kg \]](https://img.qammunity.org/2024/formulas/engineering/college/uenrj8zxvayfzqpp0mclwvd8iewqvgjjrx.png)
![\[ Q_(in) = 1.004 \cdot (1000 - 557.89) \]\[ Q_(in) \approx 446.57 \ kJ/kg \]](https://img.qammunity.org/2024/formulas/engineering/college/repvzn1x93hetlmnxu6e9igo1ts9sqqllm.png)
(c) Determine Reversibility and Entropy Generation:
The cycle is not reversible because the heat source and sink temperatures are different.
Entropy generation per unit mass:
![\[ \text{Entropy generation} = (Q_(in))/(T_(in)) - (Q_(out))/(T_(out)) \]](https://img.qammunity.org/2024/formulas/engineering/college/b00a0kz7vcxj0ea3o0rgtvpuh6ouuk8xkb.png)
Given
 and
and
 :
:
![\[ \text{Entropy generation} = (446.57)/(1200) - (459.07)/(290) \]\[ \text{Entropy generation} \approx 0.372 \ kJ/(kg \cdot K) \]](https://img.qammunity.org/2024/formulas/engineering/college/kkjnmlxgk11zpvkjiq48n80xwnhduib42g.png)
The complete question is:
An air-standard, steady-flow Brayton cycle has a pressure ratio of 15. The minimum and maximum temperatures within the cycle are 300 K and 1000 K. The pressure at the inlet to the compressor is 100 kPa. Assume the adiabatic compressor has a 90% isentropic efficiency, and
the turbine is 85% efficient compared to an isentropic one. (a) Determine the pressure and temperature of the air at the beginning of the four processes that make up the cycle. (b) Calculate the net work output of the cycle and the heat input to the air during the combustion process, both on a unit mass basis of working fluid. (c) For a constant temperature heat source of 1200 K and heat sink of 290 K, is the cycle reversible? If not, determine the entropy generation of the entire cycle per unit mass of the air. Use constant properties of air ( k = 1.4 and c_{0} = 1.004 kJ / k * g - k ).