Question

Assume that x has a normal distribution with the specified mean and standard deviation. Find the indicated probability. (Round your answer to four decimal places.)

= 2.3; = 0.38

P(x ≥ 2) =_______

Answer 1

Assume that x has a normal distribution with the specified mean and standard deviation. Find the indicated probability. (Round your answer to four decimal places.)

= 2.3; = 0.38

P(x ≥ 2) =___0.7852____

Step-by-step explanation:

The question is asking to find the probability that a normally distributed random variable x, with a mean (μ) of 2.3 and standard deviation (σ) of 0.38, is greater than or equal to 2.

To find this probability, P(x ≥ 2), you first calculate the z-score for x = 2, which normalizes the value

.

The z-score is given by the formula:

`z = (x - μ) / σ = (2 - 2.3) / 0.38 = -0.7895`

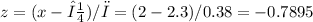
You then can look up this z-score on a standard normal distribution table or use a calculator to find the probability that z is greater than or equal to -0.7895. This gives you the probability on the right side of the mean since the normal distribution is symmetrical.

Using the z-table, you would find 1 - P(z < -0.7895) to get the desired probability, as the table provides cumulative probabilities to the left.