Question

A golfer has purchased a new driver, the Big Bertha Alpha 815. Before purchasing the new club, he averaged 350 yards per drive. He plans to take the new driver to the driving range to see if the new driver has increased or decreased the average length of his drives. He plans to hit 40 drives at the range, measure their distances, and conduct the appropriate hypothesis test with a = 0.10. The standard deviation of his drive length is 10 yards. He asks you to determine the power of this test if the driver add 5 yards to his average length. Conduct the planning phase of the hypothesis test, (a) State the hypotheses. (b) State the formula for the test statistic. (c) State the significance level. (d) Determine the critical value(s) for the test. Conduct power analysis. (e) Determine the values for the sample mean that would cause the golfer to reject the null hypothesis. ( do not submit Sketch the distribution of the sample mean when the mean distance is 350 yards and when it is 355 yards. Labela, 1-0, B. and 1.B. () Calculate the power. (h) is this a good test? Explain. How many balls must the golfer hit to drive the probability of a type Il error to 147

Answer 1

The power of the hypothesis test is the probability of correctly rejecting the null hypothesis when the true mean drive length is 355 yards.

Step-by-step explanation:

In the planning phase of the hypothesis test:

(a) State the hypotheses:

- Null Hypothesis (H₀): The average drive length with the new driver is 350 yards.

- Alternative Hypothesis (H₁): The average drive length with the new driver is greater than 350 yards.

(b) State the formula for the test statistic:

- The test statistic for a one-sample z-test is calculated as:
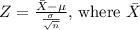`\( Z = \frac{{\bar{X} - \mu}}{{(\sigma)/(√(n))}} \), where \(\bar{X}\)`is the sample mean,
`\(\mu\)` is the population mean under the null hypothesis,
`\(\sigma\)` is the population standard deviation, and \(n\) is the sample size.

(c) State the significance level:

- The significance level
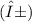`(\(α\))` is 0.10.

(d) Determine the critical value(s) for the test:

- The critical value is determined based on the chosen significance level and the nature of the test (one-tailed in this case).

(e) Determine the values for the sample mean that would cause rejection:

- Values of the sample mean greater than the critical value lead to rejection of the null hypothesis.

(f) Calculate the power:

- Power is the probability of correctly rejecting the null hypothesis. It depends on the true mean drive length, sample size, standard deviation, and significance level.

(g) Is this a good test? Explain:

- A good test has high power. Factors such as sample size, effect size, and standard deviation influence the test's power. An appropriate power ensures the ability to detect meaningful differences.

(h) How many balls must the golfer hit to drive the probability of a type II error to 1%

- Adjustments to the sample size can be made to achieve the desired level of power and control the risk of a type II error. This involves a trade-off between sample size, effect size, and significance level.