Final answer:
(a)
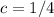
(b)
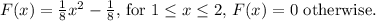
(c)
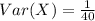
(d)

(e)
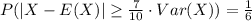
(f)
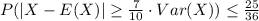
Step-by-step explanation:
(a) Constant c : To find c , we integrate f(x) over its entire range, equating it to 1 (since it's a probability density function). The integral of f(x) from 1 to 2 is
 , and setting it equal to 1, we solve for c to get
, and setting it equal to 1, we solve for c to get
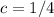 .
.
(b) Cumulative Distribution Function F(x) : Integrating f(x) from 1 to x gives the cumulative distribution function F(x) . For
 , F(x) =
, F(x) =
 otherwise.
otherwise.
(c) Variance
 : The variance of a random variable X is given by
: The variance of a random variable X is given by
![\( Var(X) = E(X^2) - [E(X)]^2 \)](https://img.qammunity.org/2024/formulas/mathematics/high-school/n7kt558ry6u5vkmdpt73cm181g043l9y54.png) . We find E(X) and
. We find E(X) and
 by integrating
by integrating
 and
and
 , respectively. The variance
, respectively. The variance
 is then calculated.
is then calculated.
(d) Variance of
 : We use the property that
: We use the property that
![\( Var(\ln(X)) = [Var(X)] / [E(X)]^2 \)](https://img.qammunity.org/2024/formulas/mathematics/high-school/nrlx9s974hyn8m2wgxcqzr2dlka3zpen6y.png) . Calculating
. Calculating
 involves finding
involves finding
 and
and
![\( E[(\ln(X))^2] \)](https://img.qammunity.org/2024/formulas/mathematics/high-school/pgbdgdkh8mpz0wef44ervwcnu71yuymhh1.png) , using the properties of logarithmic transformations.
, using the properties of logarithmic transformations.
(e) Probability
 : This involves computing the probability that X deviates from its expected value by a certain proportion of its variance.
: This involves computing the probability that X deviates from its expected value by a certain proportion of its variance.
(f) Chebyshev Inequality: Applying Chebyshev's Inequality provides an upper bound for the probability in part (e). It is given by
 , where k is the proportionality factor. For this problem,
, where k is the proportionality factor. For this problem,
 , and the upper bound is calculated as
, and the upper bound is calculated as
 .
.