Final Answer:
1. This is a one-tailed test.
2. Null hypothesis (
 : The average height of bottle rockets using pure vida water bottles is equal to or less than 150 feet. Alternative hypothesis
: The average height of bottle rockets using pure vida water bottles is equal to or less than 150 feet. Alternative hypothesis
 : The average height of bottle rockets using pure vida water bottles is greater than 150 feet.
: The average height of bottle rockets using pure vida water bottles is greater than 150 feet.
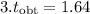
4.
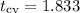
5. The null hypothesis should not be rejected.
6. The 95 percent confidence interval for the average height of bottle rockets using pure vida water bottles is

Step-by-step explanation:
In a one-tailed test, we are interested in whether the observed data falls in only one direction from the mean. In this case, the parents are investigating whether the pure vida water bottle rockets fly higher than the average, making it a one-tailed test.
The null hypothesis
 posits that the average height of bottle rockets using pure vida water bottles is equal to or less than 150 feet. The alternative hypothesis
posits that the average height of bottle rockets using pure vida water bottles is equal to or less than 150 feet. The alternative hypothesis
 suggests that the average height is greater than 150 feet.
suggests that the average height is greater than 150 feet.
To calculate
 we first find the standard deviation (S of the sample and then divide it by the square root of the sample size n. The obtained
we first find the standard deviation (S of the sample and then divide it by the square root of the sample size n. The obtained
 is then compared with the critical value
is then compared with the critical value
 for a 95 percent confidence level. If
for a 95 percent confidence level. If
 is less than
is less than
 we fail to reject the null hypothesis.
we fail to reject the null hypothesis.
The critical value
 for a one-tailed test with 7 degrees of freedom at a 95 percent confidence level is 1.833. Since
for a one-tailed test with 7 degrees of freedom at a 95 percent confidence level is 1.833. Since
 is less than
is less than
 we do not have enough evidence to reject the null hypothesis.
we do not have enough evidence to reject the null hypothesis.
Finally, the 95 percent confidence interval for the average height is calculated using the formula
 This interval provides a range within which we are 95 percent confident that the true average height lies.
This interval provides a range within which we are 95 percent confident that the true average height lies.