Question

Imagine there is a math problem that has been given to many college students across the country and the nationwide mean time to solve the problem is 110 seconds. You take a random sample of 27 students who been through a math skills workshop (to train them to solve math problems quickly) and give them this problem to solve. You believe that these students will be able to solve the problem more quickly than the national average.

a. What is the nondirectional null hypothesis in symbols? I have started it for you. H
0
​
:μ
math skills workshop students
​
b. What is the nondirectional alternative hypothesis in symbols? I have started it for you. H
1
​
: μ
math skills workshop students
​
c. With a two-tailed t-test with an alpha level of .05, and a sample of n=27, what are the degrees of freedom and the critical value of t ? Degrees of freedom = Critical value of t= d. When you test the sample of 27 students, you find that the mean time to solve the problem is 102.1 seconds and the standard deviation is 15.89 . Calculate the value of t. SHOW YOUR WORK.

Answer 1

Final Answers:

a.
`\(H_0: \mu_{\text{math skills workshop students}} = 110\)`

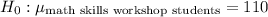
b.
`\(H_1: \mu_{\text{math skills workshop students}} \\eq 110\)`

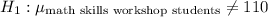
c. Degrees of freedom = 26, Critical value of t = ±2.056

d. The calculated value of t = -1.553

Step-by-step explanation:

The null hypothesis (H_0) posits that the mean time taken by students who have undergone the math skills workshop is equal to the national average time of 110 seconds. The alternative hypothesis (\(H_1\)) counters this, suggesting that the mean time for these students differs from the national average.

In this two-tailed t-test with an alpha level of 0.05 and a sample size (\(n\)) of 27, degrees of freedom are calculated as \(n - 1 = 27 - 1 = 26\). The critical value of t for a two-tailed test with 26 degrees of freedom at a 0.05 significance level is approximately ±2.056.

To compute the t-value, the formula is
`\(t = \frac{\text{sample mean} - \text{population mean}}{\frac{\text{sample standard deviation}}{√(n)}}\).`Given a sample mean of 102.1 seconds, a population mean of 110 seconds, a sample standard deviation of
`15.89, and \(n = 27\),`the calculated t-value is -1.553.

This t-value represents the difference between the mean time of the sample and the hypothesized population mean in terms of standard error units. As the calculated t-value (-1.553) falls within the range of critical values (-2.056 to +2.056), we fail to reject the null hypothesis. This means there isn't sufficient evidence to conclude that the mean time to solve the problem for math workshop students is significantly different from the national average.